Borderlands

Alright back there, time to wake up!

Four treasure-seekers find out about a mythical vault supposedly filled with a plethora of rare and valuable alien artifacts.  They travel to Pandora, a wasteland of a planet, in search of near-infinite wealth.  But they aren't the only ones searching for the vault...

---

Recommended Age Minimum Age Available On... 14 12 Xbox 360, PS3, PC, Mac Overall Fun Length Frustration   Violence Sexuality Substances Gambling 7 7 3   8 1 1 0 Mods Religion Anti-Law Community Sports Magic Miscellaneous 0 1 0 3 2 0 1

1.     Gameplay

• Overall Fun - 7

It’s odd to state that a game with gameplay that never changes is fun, but it is.  The only thing you will do in Borderlands is jump around and shoot things, but between the cooperative gameplay and the almost unlimited number of weapons this game becomes pretty addictive.

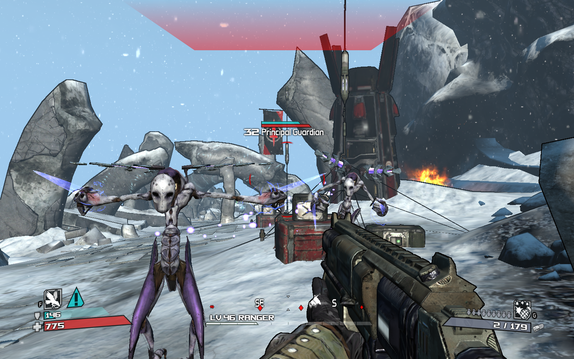
Borderlands puts the player as one of four treasure hunters on a lawless planet.  The planet is supposed to be like something from a futuristic wild west.  Many of the people, missions, environments, and props give the impression of a backwards, outlaw-based society.  The player has to try and find a mythical “vault” that is supposed to be filled with valuable alien technology.

Oh yeah, and the aliens are pissed that you want it.

That’s basically it.  The rest of the game has the player do smaller missions for money and weapons that will aid the player in the quest for the vault.  Some missions have a different overall objective, such as searching for items or killing a particular enemy, but they all involve the player running around killing dozens of enemies in the process.

Still, it’s the simplicity of the game and the amount of weapons that were included that make this game fun.  The game included a weapon-generating formula that led to the creation of hundreds of thousands of weapons.  Many weapons will look and feel slightly similar to each other, but there are some very odd weapons available.  Some weapons shoot rockets instead of bullets, others have elemental powers such as fire or electricity.  The possibilities seem almost completely endless.

Claptr4p likes to dance.

I’ve played this game twice now and had fun both times.  Cooperative gameplay is definitely a highlight of this game, so if players don’t have a friend they should try this game online.

• Length - 7

This game is fairly long.  The map is divided up into over 20 areas and each area will have at least six missions each.  Completing each mission will take time since enemies do not completely clear out of an area.  The player can eliminate the enemies in an area, but the enemies will respawn in 3 to 5 minutes.  This means that if a player has to travel deep into an area the player will have to kill enemies moving up into the area, complete the mission, and then kill more enemies coming back down.  This leads to some very repetitive gameplay.

The length of the game is primarily determined by how thorough the player is.  If the player opens every chest, locker, and mailbox in the game the game will last a few months.  This is compounded by the fact that these objects will reset once a player leaves an area and returns later.

The length will also depend on what character type the player chooses at the beginning of the game.  Mordecai the Sniper’s special ability, a hunting falcon known as “Bloodwing”, is able to attack nearby enemies.  If the player upgrades Bloodwing’s abilities to the maximum, the player will be able to mow down large groups of enemies in a matter of seconds.  Other player types, such as Lilith the Siren’s special ability is meant more as a sneaking and flanking maneuver, dealing very little damage to enemies.  This will result in a shorter average game length for Mordecai and a longer game time for Lilith.

• Frustration Factor - 3

There were only a few minor frustrations with this game.  First, the vehicle mechanics in the game were annoying at best.  If a vehicle hits any stationary object, even if it’s a slight tap, the vehicle loses all momentum.  This is a much bigger problem than it sounds.  Sometimes the player has to use his vehicle to drive away from some very strong enemies.  If the player hits an object, however, this will cause the player to come to a complete stop, making him extremely vulnerable to enemy fire.  I’ve died multiple times because I hit a small rock or the side of a metal railing.

Secondly, the system that the game uses to give items to players is a bit questionable at times.  For the most part the weapons are universal, meaning all player types can use them.  However, certain items require that a player be of a particular class in order to use them.  In my experience, the player hosting a cooperative match is much more likely to have a unique item drop for their class than any of the other classes except when that player is playing alone.  If the player is alone, he will frequently encounter elements that are meant for other player types.  The formula doesn’t seem to make much sense.

2.     Parental Notices

• Violence - 8

This games comic-like graphics make the violence fairly minor.  While enemies react to getting shot, for the most part it’s almost amusing to see them simply twitch when getting hit with dozens of rounds.

Say hello to my little friend!

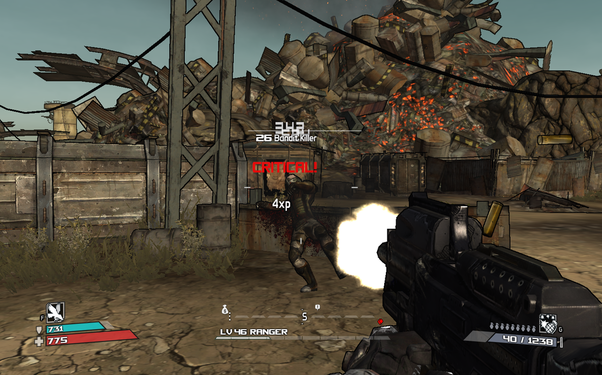
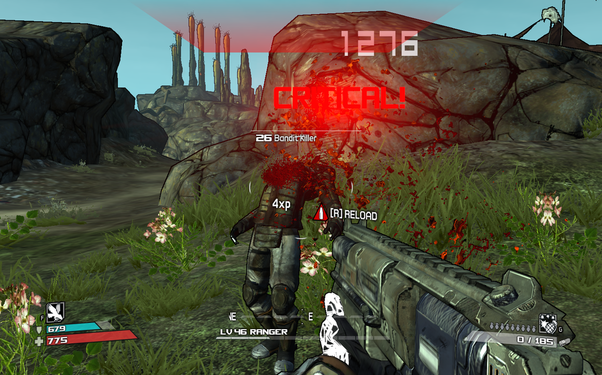
For the most part, the weapons are pretty weak and it takes dozens of rounds to take down the majority of enemies the player will face.  However, if the player hits the enemy’s weak spot, the player gets a “critical hit”.  Enemies who die from a critical hit can explode into blood depending on how hard the hit is.  Normal critical on a human enemy will cause the enemy’s head to explode and blood to rain out.

This reminds me of the end of the first Terminator movie.

Enemies that the player causes even more significant damage to will explode into a shower of blood and body parts.

Eeeewww... messy!

Some of the environments include blood, gore, and body parts as well.  It's not extremely common, but it's used to set the tone of death and destruction in appropriate locations.

Fortunately the ammunition crates are clean enough to eat on!

• Sexuality - 1

While there are no sexual images in this game, there are definitely some references to body parts.  For example, the first boss that the player faces is known as “Nine-Toes”.  When the game introduces Nine-Toes, it gives a sub-title “He also has three balls.”  Later, the player gets a mention from one of the locals mentioning that you should save another guy even though the guy ruined “his mom’s girl-parts”.

Wait, they meant ping pong balls, right? He's clearly a ping pong aficionado.

References like these are few and far between.  It’s pretty easy for a player to overlook them.  The only “nudity” is that many of the human enemies run around shirtless.  As all of the human enemies are male, this isn’t a huge deal except that many of them have metal spikes instead of nipples.  However, these are made far less noticeable when you’re simply trying to shoot them all before they hit you.

• Substances - 1

For the most part, health is provided to the player in one of two forms.  The player could use a health kit, which looks like a large white jar, or an instant health vial.  The vials look like some sort of odd injector filled with bubbling red fluid.  When the player uses health from the ground, it simply flies to the player and the player gets health.  It’s pretty rudimentary.

It's like an epi-pen, but bigger. A lot bigger.

There is one mission where you have to find alcohol for a guy.  The “booze”, as it’s called in the game, is an item that enemies in a certain area drop when they die.  No one ever drinks it, and when collected the booze flies to the player just like a normal item.

There’s no other use of substances in this game.

• Gambling - 0

There is no gambling in this game.

3.     Other Factors

• Mods - 0

The only mods available for this game seem to be save-game editors.  They’re annoying, but not “adult”.

• Religion - 1

There is one mission where bandits have started forming an organized religion.  In order to quash the religion, you are hired to burn all of the scriptures that the bandits are using.

• Anti-Law - 0

Technically this land is considered to be lawless wasteland.  I never really encountered any official law enforcement.

• Online Community - 3

Borderlands is designed to be played cooperatively with other players.  While the console versions of this game allow for split-screen, the PC version does not.  This means that almost all PC gamers and quite a few console gamers will end up playing this game with a few other people online.  This leads to one major problem, how does the game take into account that some players will be a much higher level than others?

C'mon guys, it could be worse. You could be in Black Ops.

Surprisingly, Borderlands does have a system in place that takes this problem into account.  The game awards experience points to players based on a comparison between the player’s level and the level of the enemy.  So for instance, if three level 50 players help a level 1 player take down a level 50 enemy, the level 1 player will be awarded a huge amount of experience points that will quickly help him level up.

As a result, I have never had any problems with the online community.

• Extreme Sports - 2

The player will have to learn how to drive a sort of armored dune-buggy.  The buggy will frequently have to go off huge jumps and large hills.  The player can also fall from extreme heights with minimal damage.

Brace for impact!

• Magic - 0

When the player dies, they are re-cloned back at the nearest “checkpoint”.  It’s not magical.

• Miscellaneous - 1

Excrement

One large enemy will sometimes try to use excrement based attacks to injure the player.  If the player shoots this large enemy in the behind enough, the enemy will simply try to unleash a load of acid-green stuff out of its hind quarters at the player.  However, it’s not the primary way to attack this enemy (and definitely not the smartest).  I only learned about it when a friend found a video of it on the internet.  I don’t expect the average player to ever figure it out.

Eeeeeeewwwww.

Child Killing?

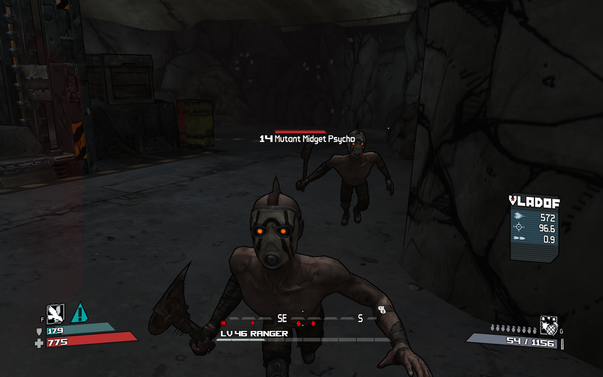
There is one recurring enemy type that seems to be a bit shady are known as "midgets".  They're pint-sized killers with very high-pitched voices.  They seem to be very buff children.

Really buff children with makeshift axes.